Finding integrals is the inverse process of finding derivatives. A function’s integral represents a family of curves. Integral calculus aids in the discovery of a function’s anti-derivatives. These anti-derivatives are also known as function integrals. Integration refers to the process of determining a function’s anti-derivative. The fundamental calculus consists of finding both derivatives and integrals.
In this topic, we will go over the fundamentals of integrals as well as how to evaluate integrals.
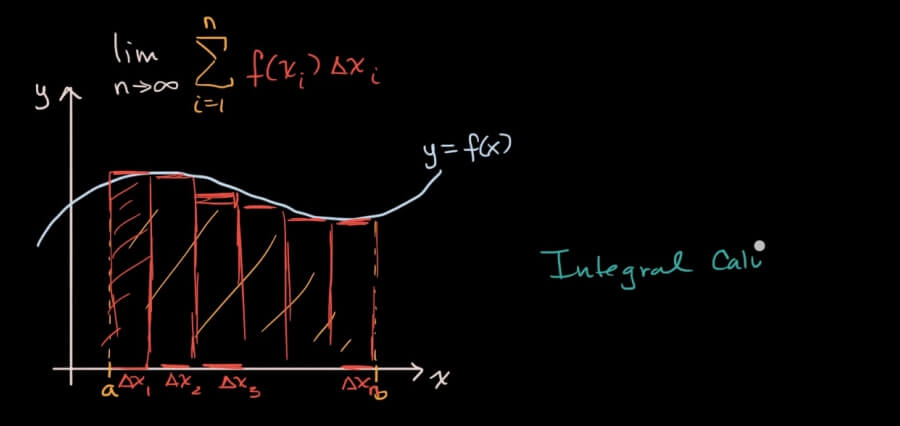
Integral Calculus Definition
Integrals are the values of the function discovered through the integration process. Integration is the process of obtaining f(x) from f'(x). Integrals assign numbers to functions in order to describe displacement and motion problems, area and volume problems, and other problems that arise from combining all of the small data. We can determine the function f using the derivative f’ of the function f. The function f is referred to as the anti-derivative or integral of f’ in this context.
What Do Integrals Mean?
An antiderivative, Newton-Leibnitz integral, or primitive of a function f(x) on an interval I is denoted by F(x). F'(x) = f(x) for all x values in I.
The area of a region under a curve is represented by an integral. By drawing rectangles, we can approximate the actual value of an integral. A definite integral of a function is defined as the area of the region bounded by the given function’s graph between two points on a line. The area of a region is calculated by dividing it into thin vertical rectangles and applying lower and upper limits. The area of the region is then added together. We define an integral of a function over an interval defined by the integral.
Types of Integrals in Calculus
Integral calculus is used to solve the following types of problems.
- a) the problem of determining the derivative of a function.
- b) the problem of determining the area bounded by a function’s graph under given conditions.
As a result, integral calculus is classified into two types.
Integrals with Definite Values (the value of the integrals are definite)
Integrals that are indefinite (the value of the integral is indefinite with an arbitrary constant, (C).
Uses of Integrals
Computations involving area, volume, arc length, the center of mass, work, and pressure are examples of integral calculus applications. Power series and Fourier series are more advanced applications. Calculus is also used to gain a more precise understanding of space, time, and motion. To understand the topic in a better and more fun way, you can visit the Cuemath website.
Uses of Integral Calculus Integral Calculus is primarily used for two purposes:
To compute f from f’. If a function f is differentiable in the interval under consideration, then the function f’ is defined. We’ve already seen how to calculate a function’s derivatives in differential calculus, and we can “undo” that with integral calculus.
To determine the area under a curve.
What are Integration Formulas?
Integration formulas can be used to integrate algebraic expressions, trigonometric ratios, inverse trigonometric functions, logarithmic and exponential functions, and other functions. The integration of functions yields the original functions for which the derivatives were calculated. These integration formulas are used to find a function’s anti-derivative. We get a family of functions in I if we differentiate a function f in an interval I. If we know the values of the functions in I, we can determine the function f. This inverse differentiation process is known as integration.
If (F(x)) = f(x), then
= F(x) + c
The function F(x) is called anti-derivative or integral or primitive of the given function f(x), and c is known as the constant of integration or the arbitrary constant.
The function f(x) is known as the integrand, and f(x)dx is called the element of integration.
Important Notes
- An integral is the primitive value of the function discovered through the integration process.
- An integral is a mathematical object that can be used to represent an area or a generalization of an area.
- The degree of the integral increases by 1 when a polynomial function is integrated.
For More Information: Click Here